- This topic has 0 replies, 1 voice, and was last updated 2 năm by
.
CFA1.FI: Công thức Duration, tính YTM?
-
Học viên 1: cô ơi câu này phần giải thích em chưa cảm thấy rõ ràng lắm ạ. EM có thử lắp vào công thức Duration để giải thích bằng cách tính YTM ra và suy luận trên công thức. Cô có thể nói rõ hơn giúp em với ạ. EM cảm ơn cô
à em vừa nhớ ra là dùng cái biểu đồ mối liên hệ giữa V và y, tính YTM của từng cái ra và plot nó lên cái đường đó
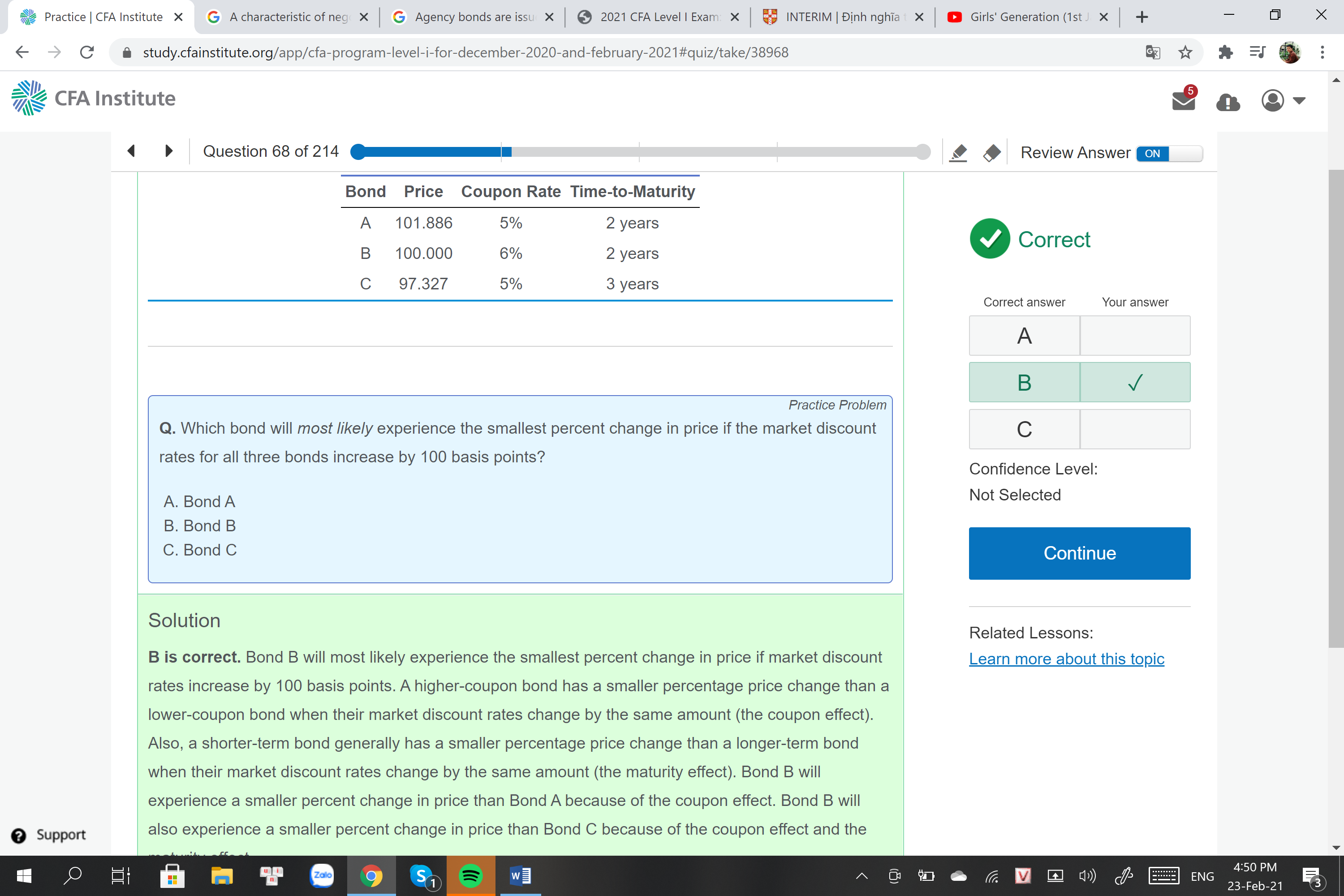
Giảng viên: tức là em không cần giải thích nữa? Bài này tìm bond nào có duration thấp nhất
Học viên 1: vâng ạ, vậy là cách giải thích mà em vừa ghi ở trên là chấp nhận được đúng không ạ?
Giảng viên: Không. Plot đó là cho 1 bond thôi, đây là 3 bonds khác nhau
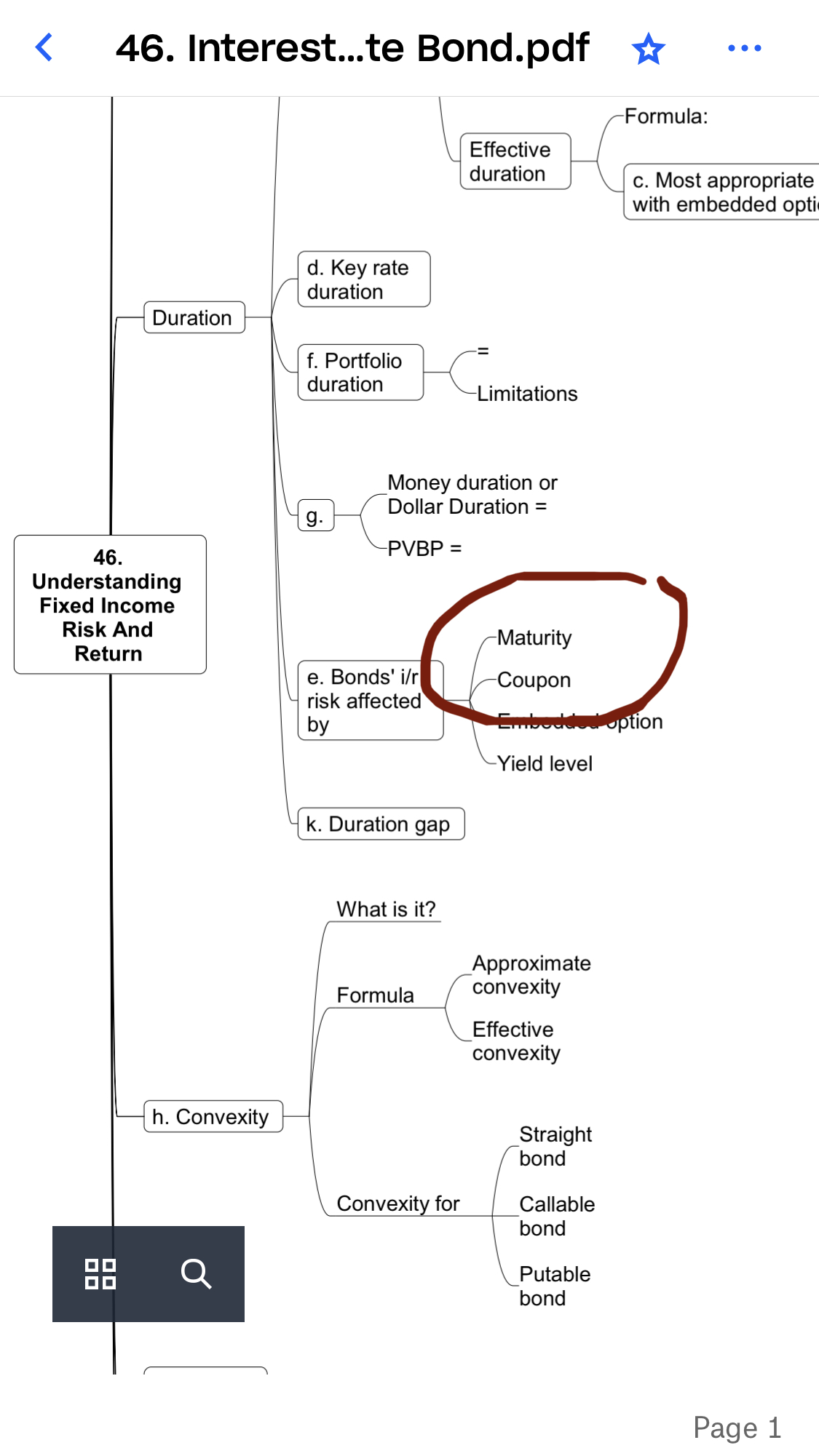
Em ôn lại relationship giữa Duration với coupon và với maturity nhé
Học viên 2: suy luận của em là Duration là đo lường rủi ro lãi suất ảnh hưởng đến giá. D giảm thì rủi ro giá biến động sẽ giảm. ở đây coupon tăng sẽ làm D giảm, time to maturiy giảm cũng là cho D giảm
Giảng viên:Chính là phần lý thuyết cô khoanh tròn nhé
Học viên 1: đây là các bond có thông số khác nhau cũng áp dụng được relationship này ạ?
Giảng viên: Em cũng có thể tính yields như em đã làm rồi tính duration của các bonds đó ra để học cho sâu
Cùng 1 bond thì maturity và coupon là cố định mà em. Nên đây là so các bonds khác nhau thì mới có thông số khác nhau được.
Học viên 1: dạ ví dụ như trong đề bài có bond A với bond B có cùng maturity nhưng mà giá và coupon rate của nó đều khác nhau, DUr bên cạnh bị ảnh hưởng bởi coupon rate thì còn bị ảnh hưởng bởi giá (theo công thức Dur) cho nên em thấy cách giải thích dựa vào relationship nó chưa thỏa đáng lắm ạ
Học viên 2: giá trị tuyệt đối thì khác nhau, nhưng ở đây là so sánh về % thay đổi nên việc khác biệt về giá trị tuyệt đối không ảnh hưởng
Giảng viên: Bạn trả lời vậy em đã ok chưa học viên 1? Công thức Duration là % giá chứ không phải giá, nên nếu đề bài có cho giá bond B là 1 triệu thay vì 100, còn giá bond A giữ nguyên 101.886, thì câu trả lời không có gì thay đổi em nhé.
Ngày 23/2/2021
.PNG?dl=0You must be logged in to reply to this topic.
